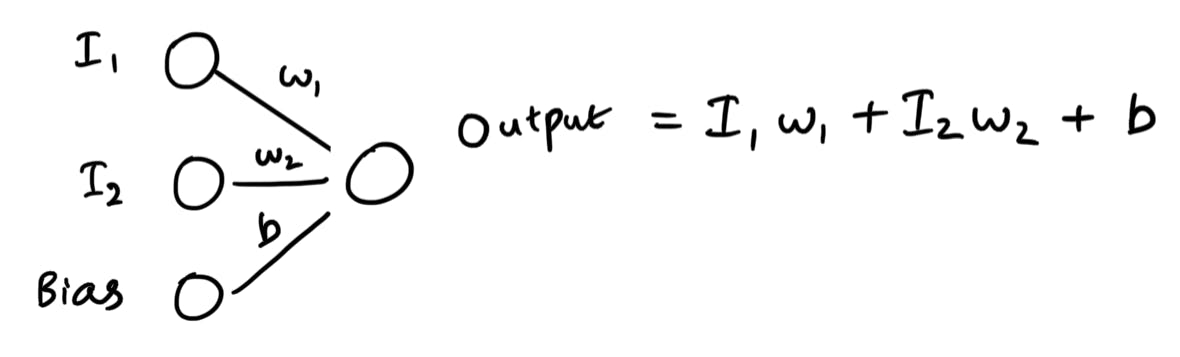Introduction
In the previous article of this series, we discussed about the types of machine learning: supervised, unsupervised and reinforcement learning.
To delve deeper into the space of ML, I will now begin exploring each type of learning in more detail, starting with supervised learning.
Even within supervised learning are several algorithms that each have their own purpose. The algorithm we are going to talk about in this article is called a neural network. So, without further delay, let's begin.
Neural networks
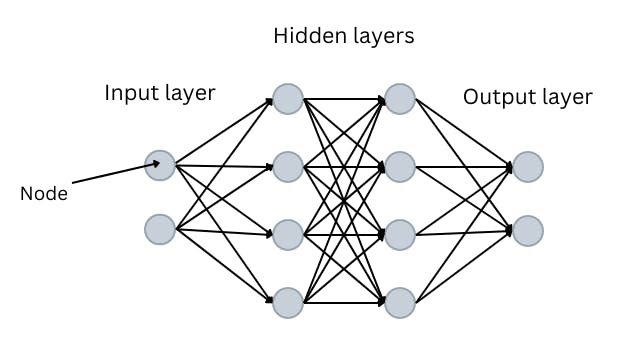
Essentially, neural networks are layers of nodes linked to give a desired output. Nodes, also called perceptrons, are units that store numerical values.
We have a layer of input nodes and a layer of output nodes. These layers are linked to each other by multiple layers in between. The layers in between are called hidden layers:
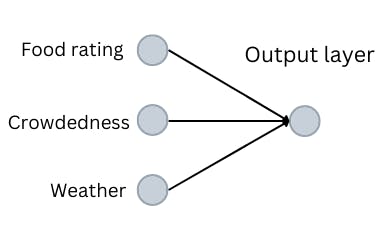
The best way to understand how neural networks work is to use an example. Say I want to determine whether or not I should eat lunch at the new pizza place in my neighborhood.
I have three parameters that will affect my decision:
- How crowdy the place is
- The food rating
- How the weather is
These are now my input nodes.
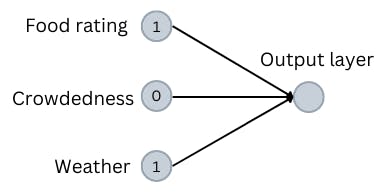
I will assign either the number zero or one for each of the above input parameters. If the place is less crowded, the food rating is high, and the weather is good, the corresponding input nodes will have a value of one. Essentially, if a factor is favorable, its value will be one. Else, its value will be zero.
For me, the food rating is the most important aspect, followed by crowdedness and weather.
Based on this knowledge, I can add weights to each parameter. This allows me to take into consideration the importance of each parameter. So, if an input has a large weight assigned to it, it would have a greater significance in determining the output (the output being whether or not I should eat at the pizza place).
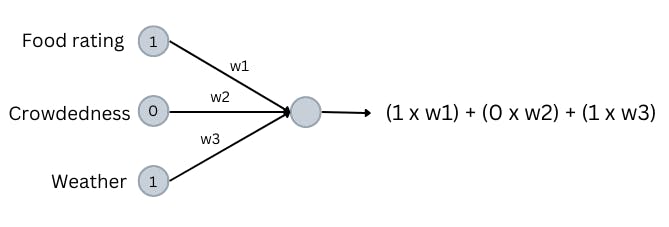
In the above diagram, w1 is the weight for the first input (food rating), w2 is the weight for the second input (crowdedness) and w3 is the weight for the third input (weather).
The output node's value can be calculated by multiplying each node's weight by the value of each node (see above diagram). Do note that this is true for any node in a neural network. Its value is the sum of the nodes in the previous layer multiplied by their corresponding weights.
Coming back to our example, the number held by the output node represents whether or not I should go out to eat lunch. If it is a high value, I should eat at the pizza place while if it is a low value, I shouldn't.
It is important for me to state that the explanations I have given so far are extremely simplistic — intended to provide an extremely general understanding of the construction of a neural network.
To develop our knowledge regarding this type of supervised learning, it's critical that I take a step back and review each process in a more detail-oriented approach.
Weights and biases
Weights are numbers that are multiplied to the value held in nodes. On the other hand, a bias is a constant number that is added to the weighted sum of a layer. So, with a bias, the value held by the output node may look something like this:
As I have already stated, weights determine the importance of a certain node in determining the final output. In our previous example, we gave the food rating a high weightage so that it would affect the output more significantly. But how do we assign a number to the weightage? How do we determine the exact numerical value we must use?
The answer is we don't. What if our neural network was extremely complex, consisting of thousands of nodes and, hence, thousands of weights? It's extremely inefficient and inaccurate if we humans decide to assign a weight to each connection.
So, when creating a neural network, we must train the model to choose reasonable weights on its own.
As I mentioned in my previous article, supervised learning involves providing data that is labelled. So, to train our neural network, we must provide training data that consists of some inputs and corresponding outputs. Using this data, the neural network will tweak the weights to improve its predictive abilities. It will also tweak the biases using this same method.
How the neural network tweaks and gets optimal weights and biases is the main focus of my next article in this series, where I will talk about how neural networks learn.
Activation function
In our pizza shop example, we stated that the value of the output node determined whether we should go out to eat or not. If it is a large number, we should visit the pizza shop. Else, we should not. But this explanation is admittedly extremely vague. There is a missing piece.
In neural networks, after taking the weighted sum of the inputs and the bias, we use an activation function. Such a function limits the output value to a range. For example, the sigmoid function transforms any number to a range between 0 and 1.
The sigmoid function is very useful as it allows us to display the output as a probability (which is always represented as a number between 0 and 1). A number close to one implies that there is a high probability of an event and a number close to zero implies there is a low probability of an event.
There exist several activation functions that convert numbers into a range of values. In the upcoming articles, we will dive into the types of activation functions and the use cases of each of them.
Conclusion
It is worth noticing that in our previous example of the pizza shop, we only had two layers in the entire neural network. In most real life applications, however, there will always be hidden layers. What is the purpose of these layers? And what decides the number of hidden layers in a neural network? I will answer all of these questions in the next few articles.
Until then, please subscribe to my newsletter to be notified regarding any updates to this series. Thank you for reading and happy coding!
Image by pch.vector on Freepik